公卫医师医学统计学辅导 直线相关

　　一、相关系数的意义

　　相关分析是用相关系数（r）来表示两个变量间相互的直线关系，并判断其密切程度的统计方法。相关系数r没有单位。在-1～+1范围内变动，其绝对值愈接近1，两个变量间的直线相关愈密切，愈接近0，相关愈不密切。相关系数若为正，说明一变量随另一变量增减而增减，方向相同；若为负，表示一变量增加、另一变量减少，即方向相反，但它不能表达直线以外（如各种曲线）的关系。

　　为判断两事物数量间有无相关，可先将两组变量中一对对数值在普通方格纸上作散点图，如图9.1～9.8所示。图中点子的分布可出现以下几种情况：

　　正相关——见图9.1，各点分布呈椭圆形，Y随X的增加而增加，X亦随Y的增加而增加，此时1>r>0.椭圆范围内各点的排列愈接近其长轴，相关愈密切，当所有点子都在长轴上时，r=1（见图9.2），称为完全正相关。

　　负相关——见图9.3，各点分布亦呈椭圆形，Y随X的增加而减少，X也随Y的增加而减少，此时0>r>-1.各点排列愈接近其长轴，相关愈密切，当所有点子都在长轴上时，r=1（见图9.4），称为完全负相关。

　　在生物现象中，完全正相关或完全负相关甚为少见。

　　无相关——见图9.5、图9.6和图9.7，X不论增加或减少，Y的大小不受其影响；反之亦然。此时r=0.另外，须注意有时虽然各点密集于一条直线，但该直线与X轴或Y轴平行，即X与Y的消长互不影响，这种情况仍为无相关。

　　非线性相关——见图9.8，图中各点的排列不呈直线趋势，却呈某种曲线形状，此时r≈0，类似这种情况称为非线性相关。

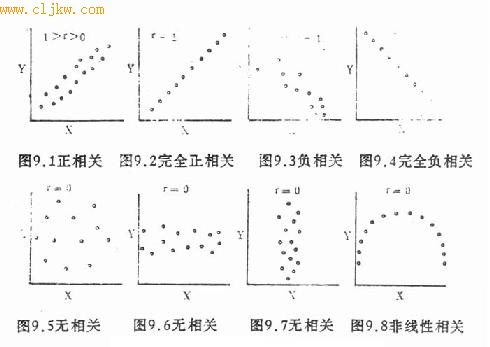
　　图9.1—9.8不同相关系数的散点示意图

　　二、相关系数的计算及假设检验

　　（一）相关系数计算法

　　计算相关系数的基本公式为：

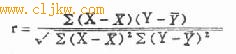
（9.1）

　　式（9.1）中r为相关系数，∑（X-X）2为X的离均差平方和，∑（Y-Y）2为Y的离均差平方和，∑（X-X）（Y-Y）为X与Y的离均差乘积之和，简称离均差积之和，此值可正可负。以此式为基础计算相关系数的方法称积差法，在实际应用时式（9.1）中各离均差平方和（简称差方和）与积之和可化为

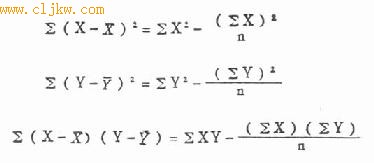
（9.2）

　　现举例说明计算相关系数的一般步骤：

　　例9.1测定15名健康成人血液的一般凝血酶浓度（单位/毫升）及血液的凝固时间（秒），测定结果记录于表9.1第（2）、（3）栏，问血凝时间与凝血酶浓度间有无相关？

　　1.绘图，将表9.1第（2）、（3）栏各对数据绘成散点图，见图9.9。

　　2.求出∑X、∑Y、∑X2、∑Y2、∑XY，见表9.1下方。

　　3.代入公式，求出r值。